在一项最新研究中，清华大学龙桂鲁、浙江大学王浩华等组成的团队创建了一种算法，仅用10个超导量子比特就实现了48位因式分解。

01 全新整数分解算法，刷新历史记录

大多数专家认为这项任务将需要数百万个量子比特。

该团队的最新实验表明，依靠整数因子化的公钥密码技术可能很快就会受到当今原始的NISQ（含噪声中等规模）量子计算机的攻击。

据研究人员称，该算法是基于经典的Schnorr算法——使用格约化来分解整数，同时依靠量子近似优化算法（QAOA）来优化Schnorr算法中最耗时的部分，以提高因式分解的速度。

研究人员表示，“使用这种算法，我们已经成功地对整数1961（11位）、48567227（26位）和261980999226229（48位）进行了因式分解，在超导量子处理器中分别使用了3、5和10个量子比特。对于48位的整数，261980999226229，我们也刷新了真正的量子设备中用一般方法算出的最大整数。”

使用这种算法的近期量子计算机可能能够处理更大的整数分解问题，可能打破广泛用于保护计算机数据和系统的RSA-2048加密方案。

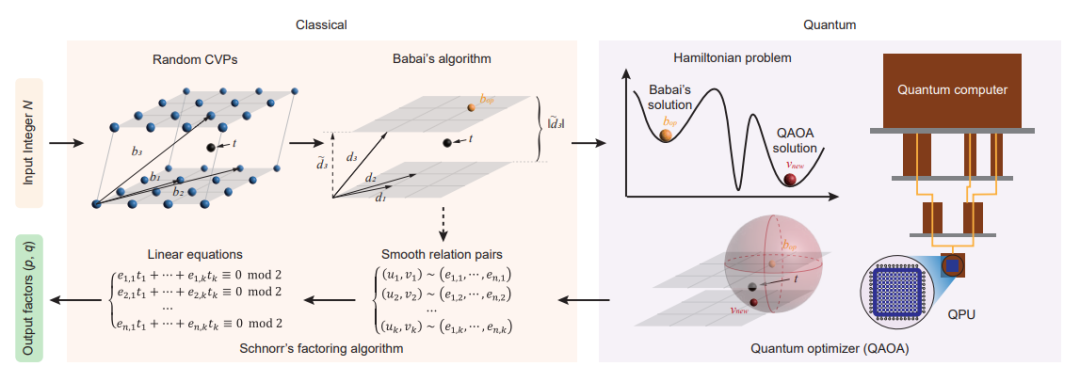
次线性资源量子整数分解（SQIF）算法的工作流。

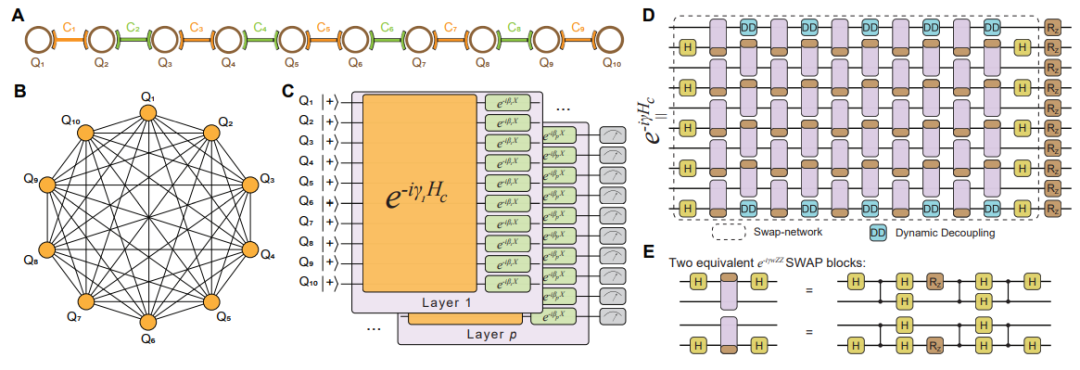
实验装置和SQIF算法的QAOA电路

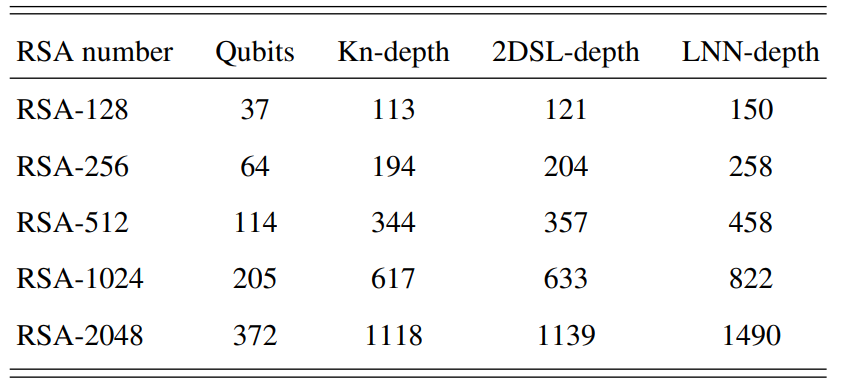
RSA数字的资源估计。提到的主要量子资源是量子比特的数量、QAOA的量子电路深度与三种典型拓扑结构的单次迭代。

02 即将在NISQ设备实现，算法加速有待确认

研究人员表示，“通过估算RSA-2048因式分解所需的量子资源来进行。我们发现，即使在最简单的一维链系统中，也需要一个具有372个物理量子比特和数千深度的量子电路来挑战RSA-2048。这样规模的量子资源最有可能在不久的将来在NISQ设备上实现。”

该团队在论文中指出，由于QAOA的收敛性不明确，该算法的量子加速还不清楚：“然而，通过QAOA优化Babai算法中的‘size-reduce’程序的想法可以作为一大批广泛使用的格约化算法中的子程序使用。进一步说，它可以帮助分析基于格的抗量子密码问题。”

该团队包括来自数学工程与先进计算国家重点实验室、清华大学、浙江大学、北京量子信息科学研究院、信息工程大学和量子信息前沿科学中心的科学家。

论文链接：

https://arxiv.org/pdf/2212.12372.pdf

参考链接：

https://thequantuminsider.com/2022/12/29/researchers-close-in-on-using-a-quantum-computer-to-crack-common-cryptographic-scheme/